Horizontal cotangent bundle
In the context of the annotation vertical bundle, we can consider that in the dual bundle $T^* E$ (the bundle "made of equations", see visualization of k-forms) we have the reciprocal version of this vertical bundle. There are equations (1-forms) which are "natural": those that define the vertical subspaces. Since they only use coordinates of the base space they constitute the "horizontal" cotangent bundle, and their sections are the horizontal 1-forms.
More info in xournal_117 and in @saunders1989geometry page 55-72.
In general, the differential forms of the total space of the fiber bundle $\pi: E\to M$ whose contraction with any vertical vector field vanish is called an horizontal 1-form or semibasic 1-form (see Bryant_2002 page xiii or @saunders1989geometry page 72). Equivalently, they are those forms whose value at $e\in E$ is the pullback via $\pi_e^*$ of a form at $\pi(e) \in M$.
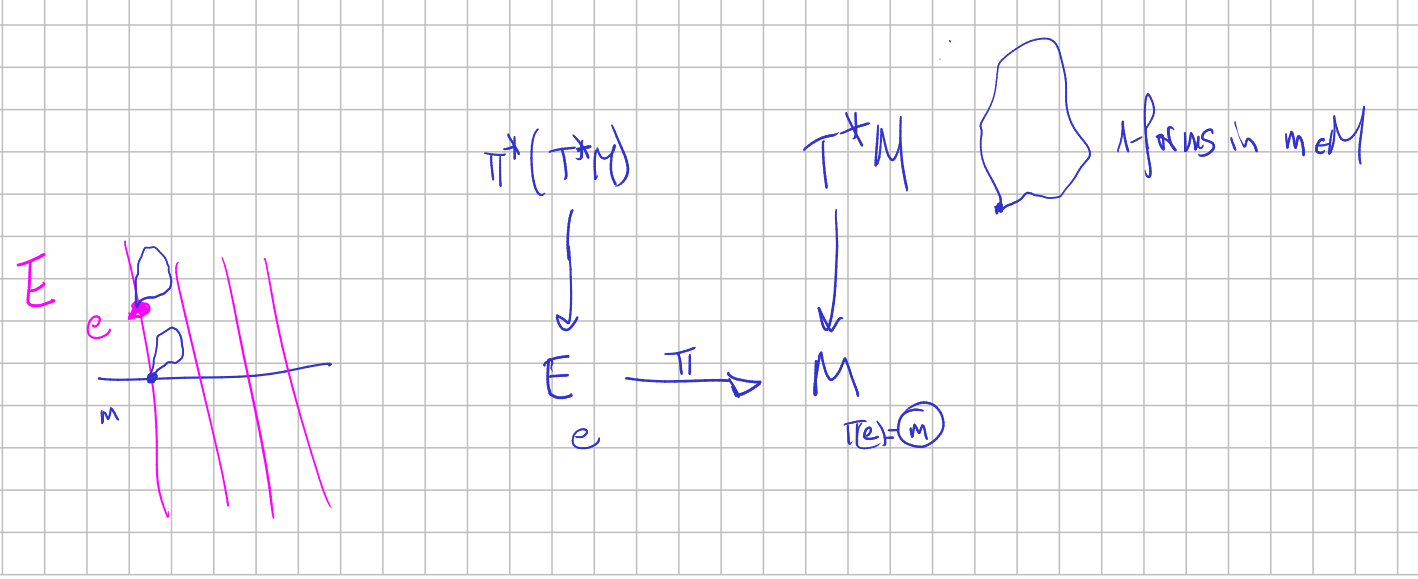
A stronger condition is that $\varphi$ be basic. It means that $\varphi$ is locally (in an open set) the pullback via $\pi^*$ of a differential form on $M$.
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: